S hierarchickými datovými strukturami se v případě vývoje webových (i desktopových) aplikací setkáváme dnes a denně. Typickými příklady mohou být např. kategorie zboží v elektronickém obchodě, strukturované menu či příspěvky v diskusním fóru.
Před každým návrhem datového modelu těchto stromových struktur se v prvé řadě potýkáme s problémem jak onu strukturu uchovávat v relační databázi. V tomto článku si blíže ukážeme výhody a nevýhody dvou možných datových reprezentací – základní parent-child strukturou a modifikovanou, postavenou na principech DFS algoritmu.
Pro zachování vzájemných vztahů mezi jednotlivými objekty v datové tabulce, jenž obsahuje běžné informace o objektu, stačí doplnit sloupec PARENT, do kterého se zapisuje primární klíč rodiče (parent) tohoto objektu. Speciálním případem jsou kořenové objekty, které nemají svého rodiče. Tuto skutečnost lze realizovat dvěma způsoby – buď uložením hodnoty 0 či (pokud to datový typ sloupce umožňuje) hodnotu NULL.
Výhodou takovéto reprezentace je jednoduché udržování struktury, kdy např. při zápisu nových položek či přesunu určitého podstromu pod jiný objekt změníme pouze hodnotu ve sloupci PARENT a nemusíme se starat o přepočítání doplňujících indexů.
Nevýhody naopak spatříme v případě požadavku na smazání určitého podstromu, kdy je nutné procházet iterativně jednotlivé úrovně podstromu a jejich mazání provést minimálně v n krocích (odpovídajících jednotlivým SQL dotazům), kde n je hloubka mazaného podstromu. Rovněž vypsání cesty k určitému objektu vede k n krokům. Opravdový problém nastává v momentě, kdy chceme v elektronickém obchodě vypsat všechny produkty přiřazené do určitého podstromu kategorií. Zde nezbývá nic jiného, než rekurzivně vyhledat všechny podkategorie vybrané kategorie, a výslednou množinu ID kategorií dát jako podmínku pro vypsání hledaných produktů. Tato operace může být v závislosti na rozvětvení stromu kategorie náročná a její provádění při každém zobrazení stránky znamená velké zatížení SQL serveru.
Tato reprezentace vychází ze základní parent-child struktury a pro efektivnější práci s daty přidává navíc sloupce LEFT a RIGHT. V těchto sloupcích se uchovávají číselné hodnoty odpovídající vstupu do a výstupu z uzlu při průchodu stromu pomocí DFS algoritmu, který vyjadřuje prohledávání stromu do hloubky. V těchto jednotlivých vyhledávacích krocích se vždy do sloupce LEFT uloží aktuální číslo kroku zvětšené o jedna. Pokud již není žádný potomek, který by šel navštívit, postupně se vracíme do vyšších úrovní a zapisujeme do sloupce RIGHT aktuální hodnotu kroku zvětšenou o jedna.
Vše lépe pochopíte z následujícího grafu kategorií PC komponent:
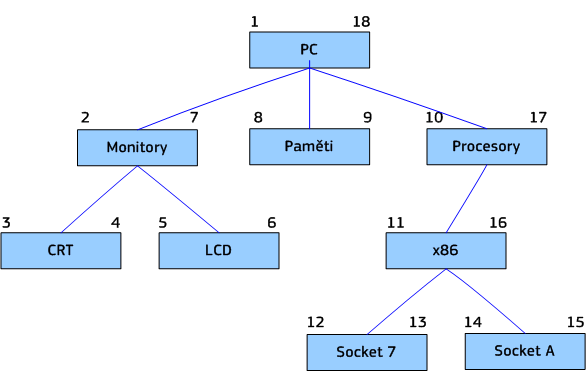
Několik užitečných vlastností DFS stromu:
Velkou výhodou při použití této reprezentace je snadné získání souvisejících objektů, které patří do určitého podstromu kategorií. Příkladem nechť nám je již několikrát avizovaný elektronický obchod a výpis všech produktů, které jsou zařazeny do aktuálním výběrem označeného podstromu kategorií. Pomocí jednoduchého dotazu nad relací kategorií a produktů, a specifikací množiny kategorií pomocí hraničních LEFT a RIGHT indexů aktuální kategorie, dostaneme všechny hledané projekty. Pomocí opačné podmínky, než v případě výpisu produktů, získáme jedním dotazem cestu k aktuální kategorii.
Poněkud větší režie je naopak potřeba při jakékoliv změně struktury (přidání uzlu, přesunutí, smazání). Až na výjimky, kdy za určitých podmínek není nutné přepočítávat všechny indexy, musíme rekurzivně projít celý strom (pomocí výše popsaného DFS algoritmu) a upravit jednotlivé indexy LEFT a RIGHT. Vzhledem k tomu, že v běžných případech dochází ke změně struktury daleko méně než k jejímu zobrazení, lze toto omezení výkonnosti brát za bezpředmětné. Další nevýhodou je existence podmínky, kdy je nutné mít indexy LEFT a RIGHT přepočítané pro určité pořadí objektů. V praxi tedy tyto struktury umožňují pouze jedno seřazení objektů, neb při každé změně řazení je nutné přepočítat celý strom a tímto bychom samozřejmě přišli o veškeré výhody při práci s těmito stromy.
S rostoucí popularitou projektu se pojí narůstající návštěvnost, do hry začínají vstupovat různé analytické nástroje, sám Google navštěvuje web ča...
Rok se s rokem sešel a v pražském Cubexu se konal další ročník konference Brand Management. Loňský rok se nesl v duchu ekonometrie, dat a Les Bine...
Do marketingového klubu Cognito přestoupili dva hvězdní hráči – Martin Veselský a Simona Matúšková. Žluto-modrý dres oblékají od konce srpna a ryc...
